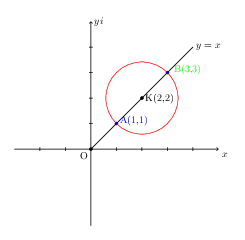Ψηφιοποιημένες ασκήσεις μαθηματικών σε html
Άσκηση 1
Έστω
$z_{1},z_{2},\dots,z_{n} \in \mathbb{C} $ έτσι ώστε να ισχύει
\begin{equation}
\Big| \frac{z_{1}-i}{z_{1}+i}\Big|+\Big|\frac{z_{2}-i}{z_{2}+i}\Big|+\cdots +\Big|\frac{z_{n}-i}{z_{n}+i}\Big|<1
\end{equation}
Να αποδείξετε ότι $\forall κ\in \{ 1,2,\dots,n \} $ ισχύει ότι $ z_{κ}\in \mathbb{C} \setminus \mathbb{R} $.
Λύση
Έστω $\exists κ \in \{ 1,2,\cdots,n \} : z_{κ} \in \mathbb{R}$. Τότε έχουμε ότι $z_{κ}-i,z_{κ}+i \in \mathbb{C}$ και μάλιστα $\overline{ z_{κ}-i }=z_{κ}+i$.
Επομένως,$ \Big|\dfrac{z_{κ}-i}{z_{κ}+i}\Big|=1 $.
Τότε όμως θα είχαμε
\begin{equation*}
\sum_{k=1}^{n} \Big| \frac{z_{κ}-i}{z_{κ}+i} \Big| \geq 1
\end{equation*}
που είναι άτοπο.
Άσκηση 2
Έστω $z \in \mathbb{C}: \mid z-(2+2i) \mid = \sqrt{2}$. Να βρεθεί ο γεωμετρικός τόπος της εικόνας του $z$ στο μιγαδικό επίπεδο.
Λύση
Έστω $z=x+iy,\quad x,y\in \mathbb{R}$. Τότε έχουμε:
\begin{eqnarray*}
|z-(2+2i)| & = & \sqrt{2} \Leftrightarrow \notag\\
|(x-2)+i(y-2)| & = & \sqrt{2} \Leftrightarrow \notag\\
(x-2)^2 + (y-2)^2 & = & 2 \notag\\
\end{eqnarray*}
Συνεπώς, ο ζητούμενος γεωμετρικός τόπος είναι ο κύκλος κέντρου Κ$(2,2)$ και ακτίνας $\sqrt{2}$.
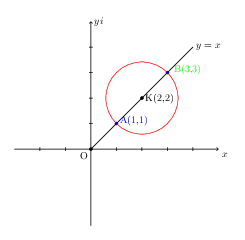
Άσκηση 3
Να βρεθεί το σύνολο των εικόνων των μιγαδικών $z$ για τους οποίους ισχύει
$$Arg \Big( \frac{z-1}{z+1} \Big)=\frac{π}{6}\nonumber$$
Λύση
Έστω $z=x+iy, \quad x,y\in \mathbb{R}$. Τότε έχουμε ότι
\begin{equation*}
\frac{z-1}{z+1}=\, \underbrace{\frac{x^2+y^2 -1}{(x+1)^2 + y^2}}_{\mathrm{Α}}\, + \, \underbrace{ \frac{2y}{(x+1)^2+y^2}}_{\mathrm{Β}} \, i
\end{equation*}
Πρέπει
\begin{equation*}
\begin{cases}
\dfrac{\mathrm{B}}{\mathrm{A}}=\tan \dfrac{π}{6} \\ \\
\mathrm{B}>0\\
\end{cases}
\end{equation*}
Άσκηση 4
Αν $ω=\cos \left(\dfrac{2π}{n}\right) + i\sin \left(\dfrac{2π}{n}\right)$, να αποδείξετε ότι:
- $1+ω+ω^2+\cdots+ω^{n-1}=0$
- $1\cdot ω\cdot ω^2\cdots ω^{n-1}=(-1)^{n-1}$
Λύση
Έχουμε $1+ω+ω^2+\cdots +ω^{n-1}=\dfrac{ 1-ω^n}{1-ω}=\dfrac{1-1}{1-ω}=0$
Έχουμε $1\, \cdot \, ω \, \cdot \, ω^2 \, \cdots \, ω^{n-1}=ω^{\frac{n(n-1)}{2}}=\dots=(-1)^{n-1}$
Άσκηση 5
Έστω $z \in \mathbb{C}: \, |z|=1$. Να βρείτε που ανήκουν οι εικόνες των μιγαδικών $w$ με $w=2z+1$.
Λύση
Αρκεί να περιγράψουμε γεωμετρικά το σύνολο $$\mathrm{A} =\{ 2z+1: z\in \mathbb{C}\, , \, |z|=1 \} \nonumber$$
Είναι $z=\dfrac{w-1}{2}$, οπότε $|z|=1 \Leftrightarrow \Bigg| \dfrac{w-1}{2} \Bigg| =1 \Leftrightarrow |w-1|=2 $
Επομένως, το σύνολο Α είναι κύκλος κέντρου Κ(0,1) και ακτίνας $\mathrm{R}=2$.