Επιχειρησιακή Έρευνα: Η συμβολή των μαθηματικών στον γραμμικό προγραμματισμό και οι σύγχρονες εφαρμογές του
Παύλος Μαργαρίτης
Τμήμα Μαθηματικών, Πανεπιστήμιο Ιωαννίνων
Εισαγωγή
Η Επιχειρησιακή Έρευνα (Operational Reasearch) είναι ο επιστημονικός κλάδος που περιλαμβάνει την ανάπτυξη και εφαρμογή επιστημονικών μεθοδολογιών
και τεχνικών με στόχο την επίλυση προβλημάτων λήψης αποφάσεων, συνήθως υπό συνθήκες που απαιτούν την κατανομή σπάνιων παραγωγικών πόρων.
Ο Μαθηματικός Προγραμματισμός είναι το σύνολο των μαθηματικών μεθόδων και υπολογιστικών τεχνικών (αλγορίθμων) που χρησιμοποιούνται για την επίλυση μιας
ειδικής κατηγορίας προβλημάτων, των προβλημάτων βελτιστοποίησης [2].
Ένα τυπικό πρόβλημα βελτιστοποίησης περιγράφεται μέσω ενός μαθηματικού μοντέλου το οποίο αποτελείται από μια πραγματική συνάρτηση της οποίας ζητείται
το μέγιστο (ή το ελάχιστο και από μια ομάδα συνθηκών που πρέπει να ικανοποιούνται από τις μεταβλητές της συνάρτησης.
Στην περίπτωση που η συνάρτηση αυτή και οι απαιτούμενες συνθήκες εκφράζονται από γραμμικές σχέσεις, τότε κάνουμε λόγο για πρόβλημα Γραμμικού
Προγραμματισμού.
Στην παρούσα εργασία θα αναλύσουμε τη συμβολή των μαθηματικών στον Γραμμικό
Προγραμματισμό, εστιάζοντας στην ιστορική εξέλιξη και στην μοντελοποίηση ενός αντιπροσωπευτικού θεωρητικού παραδείγματος εφαρμογής στην
ελαχιστοποίηση του κόστους παραγωγής. Επιπλέον θα παρουσιάσουμε εφαρμογές του Γραμμικού Προγραμματισμού σε διάφορους τομείς, καταδεικνύοντας έτσι την
σπουδαιότητα και την αποτελεσματικότητά του στην αντιμετώπιση ενός μεγάλου εύρους προβλημάτων.
Βιβλιογραφική ανασκόπηση και εφαρμογές
Βιβλιογραφική ανασκόπηση
Τα πρώτα βήματα στην ανάπτυξη της Επιχειρησιακής Έρευνας έγιναν από τον Charles Babbage(1791-1871), του οποίου η έρευνα είχε ως αντικείμενο το
κόστος μεταφοράς και ταξινόμησης της αλληλογραφίας.
Το 1917 ο Anger Krarup Erlang(1878-1929) μελέτησε προβλήματα που αφορούν τον χρόνο απασχόλησης των τηλεφωνικών κέντρων, και το 1920 ο Horace Clifford
Levinson ασχολήθηκε με προβλήματα πωλήσεων και εμπορίου.
Η Επιχειρησιακή Έρευνα αναπτύχθηκε ραγδαία κατά τη διάρκεια του Β΄ Παγκοσμίου Πολέμου, λόγω του καθοριστικου ρόλου της στον στρατηγικό σχεδιασμό, τον
εφοδιασμό και την κατανομή των πόρων [3].
Τις δεκαετίες του 1950 και 1960, αναπτύχθηκαν θεμελιώδεις αλγόριθμοι και μεθοδολογίες βασισμένοι σε μαθηματικές τεχνικές και εργαλεία, όπως η μέθοδος
του Simplex [1], που αφόρουν την επίλυση προβλημάτων Γραμμικού Προγραμματισμού.
Εφαρμογές του Γραμμικού Προγραμματισμού
Ο Γραμμικός Προγραμματισμός έχει βρει ευρύτερες εφαρμογές σε ποικίλους τομείς
[8], όπως:
- ενέργεια: βελτιστοποίηση διανομής ενέργειας, σχεδιασμός ενεργειακών δικτύων [10]
- γεωργία: βελτιστοποίηση χρήσης γης και καλλιεργειών [8]
- διαχείριση εφοδιαστικής αλυσίδας και μεταφορές: βελτιστοποίηση δρομολογίων, διαχείριση αποθεμάτων, χωροθέτηση εγκαταστάσεων [1]
- οικονομικά συστήματα: βελτιστοποίηση επενδύσεων, πιστωτικές πολιτικές [4]
- συστήματα υγείας: κατανομή ιατρικού προσωπικού και πόρων [6]
Μαθηματική περιγραφή και θεωρητικό παράδειγμα εφαρμογής
Στη συνέχεια θα εστιάσουμε στη μαθηματική διατύπωση του γενικού προβλήματος Γραμμικού Προγραμματισμού και θα παρουσιάσουμε ένα από τα πλέον σημαντικά
θεωρητικά παραδείγματα εφαρμογής στην κατανομή πόρων.
Διατύπωση γενικού προβλήματος γραμμικού προγραμματισμού - μοντελοποίηση
Ένα πρόβλημα γραμμικού προγραμματισμού μπορεί να μοντελοποιηθεί γενικά ως εξής
[2] :
Να μεγιστοποιηθεί (ή να ελαχιστοποιηθεί) η συνάρτηση $Z=c_1x_1+c_2x_2+ \dots + c_n x_n$
υπό τους περιορισμούς
\begin{align*}
a_{11}x_1 &+& a_{12} x_2 &+&\dots &+&a_{1n}x_{n} \; &\{ \leq , =, \geq \}& b{_1}\\
a_{21}x_1 &+& a_{22} x_2 &+&\dots &+&a_{2n}x_n \; &\{ \leq , =, \geq \}& b_2\\
&\vdots& &\vdots& &\vdots& &\vdots& \vdots \\
a_{m1}x_1 &+& a_{m2} x_2 &+& \dots &+&a_{mn}x_n \; &\{ \leq , =, \geq \}& b_m
\end{align*}
Τα $a_{ij},b_i,c_j , i\in \{ 1,2,\cdots ,m \}, j\in \{1,2, \cdots , n\}$ υποθέτουμε πως είναι πραγματικές σταθερές. Θεωρούμε ότι για κάθε έναν περιορισμό
μπορεί να ισχύει μόνο μία από τις σχέσεις $\leq , = , \geq$ και υποθέτουμε τη συνθήκη μη αρνητικότητας των μεταβλητών, δηλαδή ότι $x_1\geq 0 , x_2 \geq 0, \cdots , x_n \geq 0$.
Η συνάρτηση $Z$ λέγεται αντικειμενική συνάρτηση, οι συντελεστές $c_j$ αναφέρονται ως συντελεστές κέρδους (ή κόστους για προβλήματα μεγιστοποίησης)
και οι $x_1 , x_2 , \cdots , x_n$ ως συντελεστές αποφάσεων. Η περιοχή στην οποία ικανοποιούνται όλοι οι περιορισμοί λέγεται εφικτή περιοχή.
Θεωρητικό παράδειγμα εφαρμογής
Ένα παράδειγμα προβλήματος Γραμμικού Προγραμματισμού, που διαδραματίζει καθοριστικό ρόλο στην κατανομή πόρων, είναι αυτό της εύρεσης του ελάχιστου κόστους παραγωγής.
Παραθέτουμε λοιπόν το εξής παράδειγμα
[9]:
Μια εταιρία παράγει δύο προϊόντα Α και Β. Η εταιρία έχει δύο εργοστάσια ηλεκτρικών μηχανημάτων τα οποία από κοινού κατασκευάζουν τα δύο προϊόντα στις
ποσότητες ανά ώρα που φαίνονται στον ακόλουθο πίνακα:
| |
Εργοστάσιο 1 |
Εργοστάσιο 2 |
| Προϊόν Α |
10 |
20 |
| Προϊόν Β |
25 |
25 |
Η εταιρία λαμβάνει μια παραγγελία για 300 τεμάχια του προϊόντοος Α και 500 τεμάχια του προϊόντος Β. Η δαπάνη λειτουργίας του Εργοστασίου 1 είναι 10.000
ευρώ ανά ώρα, ενώ του Εργοστασίου Β είναι 8.000 ευρώ ανά ώρα.
- Να σχηματιστεί το πρόβλημα γραμμικού προγραμματισμού για την ελαχιστοποίηση του συνολικού κόστους της παραγγελίας
- Να βρεθεί το σημείο όπου ελαχιστοποιείται το κόστος, καθώς και το ελάχιστο κόστος
Λύση
Ορισμός μεταβλητών - συνθήκες:
Έστω $x_1 , x_2$ είναι ο αριθμός των ωρών κατά τις οποίες εργάζονται τα δύο εργοστάσια για την ικανοποίηση της παραγγελίας.
Tο συνολικό κόστος λειτουργίας των δύο εργοστασίων είναι $z=10.000x_1 + 8.000x_2$. Επίσης, σε μία ώρα παράγονται $10x_1+20x_2$ τεμάχια του προϊόντος Α,
και $25x_1 + 25x_2$ τεμάχια του προϊόντος Β. Εφόσον ζητούνται 300 τεμάχια του Α και 500 τεμάχια του Β, πρέπει να ισχύουν $10x_1+20x_2 \geq 300$ και
$25x_1 + 25x_2 \geq 500$. Ισχύουν επίσης $x_1 \geq 0 $ και $x_2 \geq 0$.
Μαθηματική μοντελοποίηση:
Θέλουμε να ελαχιστοποιήσουμε την αντικειμενική συνάρτηση \begin{equation*}z=10.000x_1 + 8.000x_2 \end{equation*} υπό τους περιορισμούς
\begin{align*}
10x_1 + 20x_2 \geq 300\\
25x_1 + 25x_2 \geq 500\\
x_1 \geq 0 \\
x_2 \geq 0
\end{align*}
Γραφική αναπαράσταση:
Στο παρακάτω σχήμα φαίνεται η εφικτή περιοχή του υπό μελέτη προβλήματος
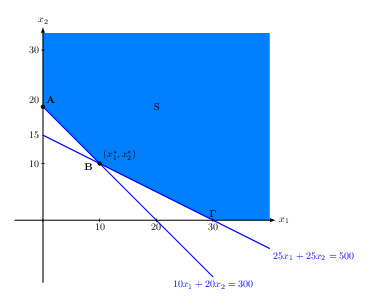
Για την εύρεση της λύσης χρησιμοποιούμε το παρακάτω θεώρημα:
Αν υπάρχει το καλύτερο διατεταγμένο ζεύγος $(x_1,x_2)$, δηλαδή το ζεύγος εκείνο που ελαχιστοποιεί (ή μεγιστοποιεί) την αντικειμενική συνάρτηση, τότε
οι τιμές $x_1$ και $x_2$ θα είναι οι συντεταγμένες $(x_1,x_2)$ ενός (ή περισσοτέρων) σημείου από τις κορυφές της εφικτής περιοχής.
Συνεπώς, προσδιορίζουμε τα σημεία Α,Β,Γ που φαίνονται στο σχήμα.
Για την εύρεση του σημείου Β, λύνουμε το σύστημα εξισώσεων:
$$\begin{cases}
25x_1 + 25x_2 = 500\\
10x_1 + 20x_2 = 300
\end{cases} \Rightarrow
\begin{cases}
x_1+x_2=20\\
x_1+2x_2=30
\end{cases} \Rightarrow
\begin{cases}
x_1=20-x_2\\
x_1+2x_2=30
\end{cases} \Rightarrow
\begin{cases}
x_1=20-x_2\\
20-x_2+2x_2=30
\end{cases} \Rightarrow
\begin{cases}
x_1=20-x_2\\
x_2=10
\end{cases} \Rightarrow
\begin{cases}
x_1=10\\
x_2=10
\end{cases}
$$
Με αντικατάσταση των σημείων Α(0,20), Β(10,10) , Γ(30,0) στην αντικειμενική συνάρτηση $z$, έχουμε:
- Για το Α(0,20) $z=10.000\cdot 0+8.000 \cdot 20 = 160.000$
- Για το Β(10,10) $z=10.000 \cdot 10 + 8.000 \cdot 20 = 180.000$
- Για το Γ(30,0) $z=10.000 \cdot 0 + 8.000 \cdot 30 = 300.000$
Συμπεράσματα:
Το σημείο Α(0,20) ελαχιστοποιεί την αντικειμενική συνάρτηση $z$ και άρα είναι η λύση του υπό μελέτη προβλήματος. Αυτό σημαίνει ότι το ελάχιστο
κόστος είναι 160.000 ευρώ και επιτυγχάνεται στο σημείο (0,20), δηλαδή όταν το Εργοστάσιο 1 δεν λειτουργεί καθόλου, ενώ το Εργοστάσιο 2 λειτουργεί
συνολικά για 20 ώρες.
Συμπεράσματα
Tα μαθηματικά διαδραματίζουν ουσιαστικό ρόλο στην επίλυση προβλημάτων Γραμμικού Προγραμματισμού και γενικότερα στην επιχειρησιακή
έρευνα, παρέχοντας ένα ισχυρό και αναλυτικό πλαίσιο για την ανάλυση και την μοντελοποίηση. Η ευρεία εφαρμογή του Γραμμικού Προγραμματισμού στη διαχείρηση των αποθεμάτων, στην παραγωγή και
στις μεταφορές, στα χρηματοοικονομικά και σε πολλούς άλλους τομείς, καταδεικνύει την τεράστια αξία και την αναγκαιότητα του. Η συνεχής ανάπτυξη
νέων μεθοδολογιών και υπολογιστικών εργαλίων αναμένεται να επηρρεάσει καταλυτικά την αντιμετώπιση ενός μεγάλου εύρους σύνθετων προβλημάτων στο μέλλον.
Αναφορές
- [1]
- Ηillier, Frederick and Lieberman, Gerald. Εισαγωγή στην Επιχειρησιακή Έρευνα. Τζιόλα,2017
- [2]
- Δημήτρης Φακίνος και Αντώνης Οικονόμου. Εισαγωγή στην Επιχειρησιακή Έρευνα. Εκδόσεις Παπαζήση, 2022.
- [3]
- Ιωάννης Κολέτσος κα Δημήτρης Στογιάννης. Επιχειρησιακή Έρευνα. Συμεών, 2021.
- [4]
- Κωνσταντίνος Κουνέτας. Εισαγωγή στην Επιχειρησιακή Έρευνα και στον Γραμμικό Προγραμματισμό.Λύσεις προβλημάτων με το πρόγραμμα R. Κάλλιπος, 2016.
- [5]
- Δημήτρης Μάγος. Στοιχεία γραμμικού και ακέραιου προγραμματισμού. Κάλλιπος, 2023.
- [6]
- Κωνσταντίνος Παππαρίζος. Γραμμικός Προγραμματισμός Αλγόριθμοι και Εφαρμογές. Ζυγός, 1999.
- [7]
- Ιωάννης Ρασσιάς. Γραμμική Άλγεβρα - Γραμμικός Προγραμματισμός. Συμμετρία, 2003.
- [8]
- Παντελής Υψηλάντης. Επιχειρησιακή Έρευνα. Προπομπός, 2007.
- [9]
- Φράγκος, Χρήστος Κ. Εισαγωγή ατην Επιχειρησιακή Έρευνα. Σταμούλη Α.Ε., 2006.
- [10]
- Κωνσταντίνος Κουνέτας και Νικόλαος Χατζησταμούλου Εφαρμοσμένη επιχειρησιακή έρευνα και γραμμικός προγραμματισμός. Κριτική, 2020.

