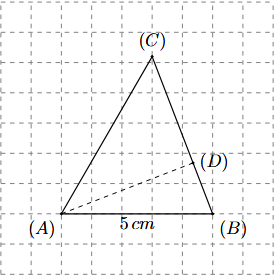
Να λυθεί η διαφορική εξίσωση: $y' = \frac{1}{2e^{y}-x}$
Η δοθείσα διαφορική εξίσωση δεν είναι γραμμική. Εναλλάσοντας όμως, το ρόλο των μεταβλητών και θεωρόντας το x ως συνάρτηση του y, προκύπτει ότι:
η οποία είναι γραμμική εξίσωση ως προς το x(y). Έτσι, απο την (1) έχουμε \[\frac{d}{dx}(xe^{y})=2e^{2y}, \notag\] οπότε \[xe^{y} = e^{2y} + C, \notag\] ή
όπου C είναι μια αυθαίρετη πραγματική σταθερά. Η σχέση (2) δίνει τη γενική λύση της αρχικής διαφορικής εξίσωσης σε πεπλεγμένη μορφή.
Δίνεται τρίγωνο ABC με πλευρές $AB=5 \text{cm}, AC = 6 \text{cm},$
και γωνία $\angle BAC = 60^{^{\circ}}$.
Να σχεδιάσετε το τρίγωνο και να φέρετε το ύψος απο το σημείο Α στην πλευρα BC.
Να υπολογιστεί το μήκος του ύψους.
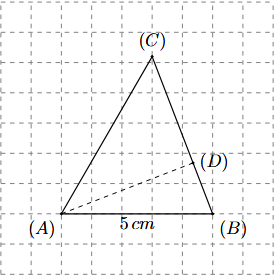
Γνωρίζουμε ότι: \[ h = AC \cdot \sin(\angle BAC) = 6 \cdot \sin(60^{^{\circ}}) = 6 \cdot \frac{\sqrt{3}}{2} = 3\sqrt{3} \approx 5.20 \, \text{cm} \notag \] Άρα. το ύψος από το Α στην πλευρά BC είναι περίπου $\boxed{5.20 \, \text{cm}}$
Να παρασταθεί γραφικά η συνάρτηση $f(x) = x^2 -2x -3$ και να προσδιοριστούν οι ρίζες, το ελάχιστο και το σημείο τομής με τον άξονα y.
Έχουμε τη συνάρτηση:

Οι ρίζες της συνάρτησης (3) είναι οι τιμές του x για τις οποίες ισχυεί: \[ f(x) = 0 \Rightarrow x^2 -2x -3 = 0 \notag \] Εφαρμόζουμε τον τύπο επίλυσης δευτεροβάθμιας εξίσωσης: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \notag \] όπου $a=1, b=-2, c=-3$. Υπολογίζουμε: \[ x = \frac{-(-2) \pm \sqrt{(-2)^2 -4\cdot 1 \cdot (-3)}}{2 \cdot 1} = \frac{2 \pm \sqrt{4 + 12}}{2} = \frac{2 \pm \sqrt{16}}{2} = \frac{2 \pm 4}{2} \notag \] Άρα:
Οι ρίζες της συνάρτησης είναι: \[ x=-1 \text{ και } x=3 \notag \] Η γραφική παράσταση της συνάρτησης είναι παραβολή με φορά προς τα πάνω, αφού ο συντελεστής του $x^2$ είναι θετικός.
Η x-συντεταγμένη της κορυφής του ελαχίστου δίνεται από τον τύπο:
\[
x_0 = \frac{-b}{2a} = \frac{-(-2)}{2\cdot 1} = \frac{2}{2} = 1 \notag
\]
Αντικαθιστούμε στην $f(x)$ για να βρούμε το ελάχιστο:
\[
f(1) = (1)^2 -2 \cdot 1 -3 = 1-2-3 = -4 \notag
\]
Άρα το ελάχιστο της συνάρτησης είναι στο σημείο $(1, -4)$
Η τομή με τον άξονα y γίνεται όταν $x=0$:
\[
f(0) = 0^2 -2\cdot 0 -3 = -3 \notag
\]
Άρα η συνάρτηση τέμνει τον άξονα y στο σημείο: $(0, -3)$
Αν $A = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ υπολογίστε τον πίνακα $A^n$.
Άρα: \begin{align} A^n &= \begin{cases} I_2, & n=4k \\ A, & n=4k+1, \\ -I_2, & n=4k+2,\\ -A, & n=4k+3 \end{cases} \qquad ,k \in \mathbb{N} \notag \end{align}
Αν $\vec{u}, \vec{v}, \vec{w}$ είναι γραμμικώς ανεξάρτητα διανύσματα του $\mathbb{R}^3$ δείξτε ότι και τα $\vec{u} + 2\vec{v} + 4\vec{w}, 2\vec{v} + 5\vec{u} + \vec{w}, 3\vec{u} + \vec{w}$ είναι επίσης γραμμικώς ανεξάρτητα διανύσματα.
Έστω $k, \lambda, \mu \in \mathbb{R}$ τέτοια ώστε \[ k\cdot (\vec{u} + 2\vec{v} + 4\vec{w}) + \lambda \cdot (2\vec{v} + 5\vec{u} + \vec{w}) + \mu \cdot (3\vec{u} + \vec{w}) = \vec{\mathbf{0}}. \notag \] Τότε \[ (k +5\lambda +3\mu) \cdot \vec{u} + (2k + 2\lambda) \cdot \vec{v} + (4k + \lambda + \mu) \cdot \vec{w} = \vec{\mathbf{0}}. \notag \] Επειδή τα $u,v,w$ είναι γραμμικώς ανεξάρτητα εξ ορισμού το σύστημα εξισώσεων \[ \begin{cases} k + 5\lambda +3\mu = 0 \\ 2k +2\lambda = 0 \\ 4k + \lambda + \mu = 0 \notag \end{cases} \] πρέπει να έχει μοναδική λύση τη μηδενική. Το σύστημα αυτό είναι ομογενές $3 \times 3$ σύστημα. Επειδή η ορίζουσα των συντελεστών των αγνώστων ικανοποιεί την \[ \begin{vmatrix} 1 & 5 & 3 \\ 2 & 2 & 0\\ 4 & 1 & 1 \end{vmatrix} = -26 \neq 0 \notag \] συμπεραίνουμε ότι το σύστημα έχει μοναδική λύση τη μηδενική $k= \lambda = \mu =0 $. Άρα τα $\vec{u} + 2\vec{v} +4\vec{w}, 2\vec{v} + 5\vec{u} + \vec{w}, 3\vec{u} + \vec{w}$ είναι γραμμικά ανεξάρτητα.