Στην επιστήμη της πληροφορικής, οι μέγιστες ροές και τα ταιριάσματα (ή αλλιώς αντιστοιχίσεις) είναι δύο βασικά προβλήματα της Θεωρίας Γραφημάτων με πληθώρα εφαρμογών, τόσο θεωρητικών όσο και πρακτικών. Αν και εκ πρώτης όψεως φαίνονται διαφορετικά προβλήματα, υπάρχει μια βαθιά μαθηματική συσχέτιση μεταξύ τους και αυτή η σχέση είναι άξια διερεύνησης για λόγους που θα αναλυθούν παρακάτω.
Μέγιστες Ροές (Maximum Flows)Το πρόβλημα της μέγιστης ροής αφορα ένα κατευθυνόμενο γράφημα όπου κάθε ακμή έχει μία χωρητικότητα. Σε αυτή, θέλουμε να υπολογίσουμε την μέγιστη ροή που μπορεί να περάσει από μία πηγή (source) προς ένα στόχο (sink) χωρίς να παραβιάζονται οι περιορισμοί χωρητικότητας.
Μερικά παραδείγματα εφαρμογών που έχουν ως κύριο θέμα τους την μέγιστη ροή αποτελούν:
Ένα ταίριασμα σε ένα απλό γράφημα είναι ένα σύνολο από ακμές που δεν έχουν κοινές κορυφές, δηλαδή, κάθε κορυφή συμμετέχει το πολύ σε μία ακμή του ταιριάσματος. Το πρόβλημα μέγιστου ταιριάσματος (maximum matching) ζητά το μεγαλύτερο δυνατό τέτοιο σύνολο. Στα διμερή γραφήματα (bipartite graphs), το πρόβλημα έχει ιδιαίτερο ενδιαφέρον και πιο αποτελεσματικές λύσεις.
Κάποια από τα παραδείγματα εφαρμογών απότελουν:
Η βασική ιδέα που αφορά την συσχέτιση των δύο αυτών εννοιών προκύπτει από το παρακάτω Θεώρημα:
και πάνω σε αυτό θα βασιστεί η θεωρητική μας διερεύνηση.
Η μελέτη της σχέσης μεταξύ προβλημάτων μέγιστης ροής και ταιριάσματος έχει απασχολήσει την επιστημονική κινότητα εδώ και δεκαετίες. Το θεμέλιο τέθηκε από τους Ford και Fulkerson [4], οι οποίοι εισήγαγαν τον πρώτο γενικό αλγόριθμο μέγιστης ροής και έδειξαν πώς προβλήματα συνδυαστική φύσης μπορούν να διατυπωθούν ως προβλήματα ροής. Στη συνέχεια, ο Hopcroft και ο Karp [3] ανέπτυξαν έναν εξειδικευμένο αλγόριθμο για μέγιστο ταίριασμα σε δίπλευρους γράφους, βελτιώνοντας σημαντικά την υπολογιστική αποδοτικότητα με πολυπλοκότητα $O\left( \sqrt{V} \cdot E \right)$.
Η συσχέτιση των δύο προβλημάτων αξιοποιείται ευρέως στη σχεδίαση αλγορίθμων, όπως περιγράφεται και στο έργο των Cormen et al [2], όπου γίνεται λεπτομερής ανάλυση του τρόπου μετασχηματισμού ενός προβλήματος ταιριάσματος σε πρόβλημα ροής. Περαιτέρω εφαρμογές και γενικεύσεις της θεωρίας βρίσκονται σε πιο προχωρημένες πηγές όπως το έργο των Korte και Vygen [5-7], όπου αναδεικνύονται οι προεκτάσεις της στη συνδυαστική βελτιστοποίηση και την επιχειρησιακή έρευνα.
Πιο πρόσφατα, η έρευνα έχει επικεντρωθεί στη βελτίωση της υπολογιστικής αποδοτικότητας μέσω νέων συνδυαστικών τεχνικών και μοντέλων μάθησης. O Chuzhoy και ο Khanna [1] παρουσίασαν έναν ταχύτερο αλγόριθμο μέγιστου ταιριάσματος για πυκνά γραφήματα, ο οποίος μειώνει την πολυπλοκότητα κάτω από εκείνη του Hopcroft-Karp σε συγκεκριμένες περιπτώσεις. Παράλληλα, η εφαρμογή Graph Neural Networks (GNNs) έχει δείξει ότι μπορςί να προσεγγίσει το μέγιστο ταίριασμα με μεγάλη ακρίβεια, ακόμα και σε πολύ μεγάλα γραφήματα. Ο Li et al [11] πρότειναν ένα GNN-based μοντέλο που μαθαίνει τον υποκείμενο συνδυαστικό κανόνα και αποδίδει καλύτερα σε πολλές ρεαλιστικές περιπτώσεις απ΄ό,τι οι παραδοσιακοί αλγόριθμοι.
Οι όροι που χρειαζόμαστε για ανάλυση και κατανόηση αυτού του θέματος περιέχουν:
Ταίριασμα: Σε ένα γράφημα $G=(V,E)$, το ταίριασμα Μ είναι ένα υποσύνολο
όλων των ακμών έτσι ώστε καμία κορυφή $u \in V$ να μην χρησιμοποιείται από περισσότερες από μία ακμές του Μ.
Μέγεθος ταιριάσματος: Ο αριθμός των ακμών που περιέχει το ταίριασμα: $|M|$.
Μέγιστο ταίριασμα: Αυτό του οποίου το μέγεθος $|M|$ είναι το μέγιστο.
Διμερές γράφημα: Γράφημα $G=(A,B,E)$ στο οποίο το σύνολο
των κορυφών $v$ χωρίζεται σε 2 ξεχωριστά σύνολα Α και Β και όλες οι ακμές Ε συνδέουν κορυφή του Α με κορύφες του Β μόνο.
Μετασχηματισμός του διμερούς γραφήματος $G$ σε δίκτυο ροής $Ν=(H,c,s,t)$:
Σε αυτή την ενότητα θα υλοποιήσουμε ένα παράδειγμα πάνω σε αυτές τις έννοιες, το οποίο θα τις συνδέσει μεταξύ τους. Το πρόβλημα αυτό είναι το εξής:
Σε αυτή την άσκηση, επιθυμούμε την εύρεση ενός μέγιστου ταιριάσματος ενός διμερούς γραφήματος $G=(A,B,E)$, δηλαδή ενός γραφήματος του οποίου το σύνολο κορυφών μπορεί να διαμερισθεί σε δύο σύνολα Α και Β έτσι ώστε $E \subseteq A \times B$. Για το σκοπό αυτό, βασιζόμενοι στο γράφημα $G$ κατασκευάζουμε ένα δίκτυο ροής $N=(H,c,s,t)$:
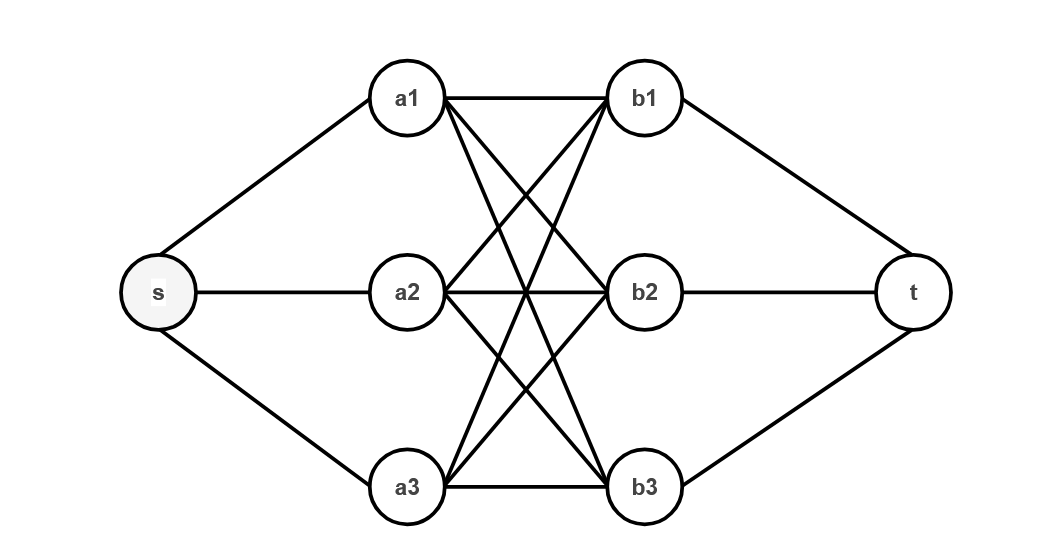
Το πλήρες διμερές γράφημα $K_{3,3}$ έχει τα σύνολα κορυφών $A=\{a_1,a_2,a_3\}$ και $B=\{b_1,b_2,b_3\}$ κα κάθε κορυφή του Α συνδέεται με όλες τις κορυφές του Β. Δηλαδή: $E=\{(a_i,b_j)|i,j \in \{1,2,3\} \}$
Για να το μετασχηματίσουμε σε δίκτυο ροής $N=(H,c,s,t)$:
Η αναπαράσταση μέσω γραφήματος:
Η πηγή $s$: συνδέεται με ακμή με τις κορυφές του Α: $a_1,a_2,a_3$
Οι κορυφές του $Α$: συνδέονται όλες με όλες τις κορυφές του Β: $b_1,b_2,b_3$
Οι κορυφές του $Β$: συνδέονται με ακμή με τον προορισμό $t$

Η μελέτη της σχέσης μεταξύ μέγιστων ροών και ταιριάσματος σε διμερή γραφήματα ανέδειξε μια ιδιαίτερα χρήσιμη κατασκευή, μέσω της οπίας ένα πρόβλημα
συνδυαστικής φύσης μπορεί να λυθεί με εργαλεία της θεωρίας ροής και γραφημάτων. Συγκεκριμένα, μετασχηματίσαμε ένα πρόβλημα μέγιστης ροής μονάδας, κατασκευάζοντας το αντίστοιχο δίκτυο ροής με τεχνητή πηγή και προορισμό.
Στο παράδειγμα του πλήρους διμερούς γραφήματος $Κ_{3,3}$ το οποίο περιέχει
6 κορυφές και 9 ακμές, το αντίστοιχο δίκτυο ροής περιλαμβάνει 8 κορυφές
$(A \cup B \cup \{s,t\})$ και 15 ακμές όλες χωρητικότητα ίση με ένα.
Η μέγιστη ροή από την πηγή s ως τον προορισμό t ισούται με 3, δηλαδη το μέγεθος
του μέγιστου ταιριάσματος.
Αυτό το παράδειγμα αποδεικνύει με πρακτικό τρόπο το θεωρητικό θεώρημα που συνδέει τα μέγιστα ταιριάσματα σε διμερή γραφήματα με προβλήματα μέγιστης
ροής μονάδας. Επιπλέον, η προσέγγιση αυτή προσφέρει μια υπολογιστικά αποδοτική
μέθοδο επίλυσης τέτοιων προβλημάτων, αξιοποιώντας υπάρχοντες αλγόριθμους ροής
(π.χ. Edmonds-Karp). Η τεχνική είναι γενικεύσιμη και εφαρμόσιμη σε πολλά προβλήματα
στην πραγματική ζώη, όπως κατανομές εργασιών, δρομολόγηση και σύστημα συστάσεων [8-10].