Ασκηση 1:
Να υπολογιστούν τα ολοκληρώματα:
(α)
$$
\int \frac{6x^3+x^2-2x+1}{2x-1}\,dx
$$
(β)
$$
\int \frac{dx}{\sin^2x\cos^2x}
$$
(γ)
$$
\int \frac{dx}{\sqrt{5-x^2-4x}}
$$
Λύση
(α)
Εχουμε $ \frac{6x^3+x^2-2x+1}{2x-1}=3x^2+2x+\frac{1}{2x-1},\quad$ οπότε θα είναι
$$
\int \frac{6x^3+x^2-2x+1}{2x-1}\,dx = \int(3x^2+2x)\,dx+\int\frac{dx}{2x-1}=x^3+x^2+\ln\left|2x-1\right|+c ,\quad \\
x\in\left(-\infty,\quad\frac{1}{2}\right)\cup\left(\frac{1}{2},\quad\infty\right).
$$
(β)
$$
\int \frac{dx}{\sin^2x\cos^2x}=4\int\frac{dx}{\sin^2{2x}}=-2\cot{2x}+c,\quad x\ne k\pi,k\in \mathbb{Z}
$$
(γ)
$$
I=\int\frac{dx}{\sqrt{5-x^2-4x}}=\int\frac{dx}{\sqrt{9-(x+2)^2}}=\frac{1}{3}\int \frac{dx}{\sqrt{1-\left( \frac{x+2}{3} \right)^2}}
$$
Αν θέσουμε $ \frac{x+2}{3}=t $,\quad τότε $x+2=3t$ και $dx = 3dt ,\quad$
οπότε έχουμε
$$
I=\frac{1}{3}\int\frac{3dt}{\sqrt{1-t^2}}=\arcsin t +c=\arcsin\left(\frac{x+2}{3}\right)+c,\quad
$$
όπου $ x\in J = \left\{x:\left|x+2\right| < 3 \right\}=\left(-5,\quad1\right) $
note: οι ασκήσεις ειναι απο το αρχείο paradeigmata_askiseon_mathjax.docx που είναι ανεβασμένο στο spooky.
Ασκηση 2:
Να αποτυπωθεί ο ακόλουθος πίνακας σε γράφημα με χρήση tikz
| speedup | 1 | 2 | 3 | 4 |
|---|
| 1000 | 10.39372325 | 10.10540915 | 9.574244415 | 8.858358663 |
| 2000 | 84.91593476 | 103.9600614 | 108.1694193 | 105.5819033 |
| 3000 | 134.1270928 | 206.6760481 | 47.3585965 | 266.2280967 |
| 4000 | 167.7174254 | 289.8229908 | 376.431623 | 430.2481752 |
| 5000 | 171.3004226 | 315.9734197 | 433.1362173 | 526.3092929 |
| 6000 | 190.1277774 | 360.6296115 | 505.1097613 | 635.0680865 |
Λύση
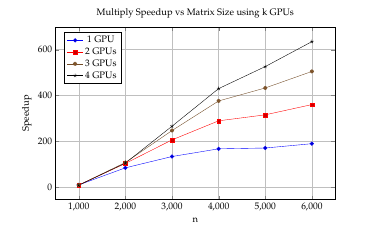
Ασκηση 3:
Δίνεται ορθογώνιο τρίγωνο ABC με AB=3 και AC=4. Να βρεθούν η υποτείνουσα και το εμβαδόν του τριγώνου, καθώς και να σχεδιαστεί.
Λύση:
Γνωρίζουμε από το Πυθαγόρειο Θεώρημα ότι αν BC η υποτείνουσα, τότε ισχύει:
$$
BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=\sqrt{25}=5
$$
άρα η υποτείνουσα του τριγώνου ABC είναι $BC=5$. Για το εμβαδον του τργώνου τώρα γνωρίζουμε ότι ισχύει ο τύπος:
$$
Ε = \frac{βαση * υψος}{2}
$$.
Αρα έχουμε:
$$
(ABC)=\frac{AC*AB}{2}=\frac{3*4}{2}=6
$$
Ασκηση 4:
Να βρεθεί που συγκλίνει η ακόλουθη σειρά:
$$
\sum_{k=1}^{\infty}\frac{k!}{k^k}
$$
Λύση:
Για την παραπάνω σειρά ισχύει ότι $a_k \ge 0$. Εχουμε:
$$
\left|\frac{a_{k+1}}{a_k} \right|=\frac{(k+1)!}{k!}*\frac{k^k}{(k+1)^{k+1}}=\frac{1*2*3*\cdots*k(k+1)*k^k}{1*2*3**\cdots*(k+1)^k*(k+1)}= \\
\left(\frac{k}{k+1}\right)^k = \left(\frac{1}{1+\frac{1}{k}}\right)^k \to \frac{1}{e}<1
$$
άρα από Κριτήριο Λόγου η
$$
\sum_{k=1}^{\infty}a_k
$$ συγκλίνει.
Ασκηση 5
Υπολογίστε το ακόλουθο όριο: $$ \lim_{x\to0}\left(\frac{1}{x^2}-\frac{1}{sin^2x}\right) $$
Λύση
Γραφουμε την παράσταση ως εξής:
$$
\frac{1}{x^2}-\frac{1}{sin^2x}=\frac{sin^2-x^2}{x^2*sin^2x}
$$
Αναπτύσσουμε το $\sin(x)$ σε σειρά Taylor γύρω από το 0:
$$
\sin(x)=x-\frac{x^3}{6}+\frac{x^5}{120}-\cdots
$$
και επομένως
$$
sin^2x=\left(x-\frac{x^3}{6}+\frac{x^5}{120}-\cdots\right)^2=x^2-\frac{x^4}{3}+\cdots
$$
Αρα:
$$
sin^2x-x^2=-\frac{x^4}{3}+\cdots
$$
Οπότε η αρχική παράσταση γίνεται:
$$
\frac{-\frac{x^4}{3}+\cdots}{x^2\left(x^2-\frac{x^4}{3}+\cdots\right)}=
\frac{-\frac{x^4}{3}+\cdots}{x^4+\cdots}
$$
Καθώς $x\to0$,τα υψηλότερης τάξης μέλη τείνουν στο 0 και έτσι εν τέλει έχουμε ότι:
$$
\lim_{x\to0}\left(\frac{1}{x^2}-\frac{1}{sin^2x}\right)=-\frac{1}{3}
$$
