΄Εχουμε τις εξής παραμέτρους:
![P = ------------1------------
0 ∑cn-=10[ 1n!(λμ)n]+ 1c!(λμ)c(ccμμ-λ)](hw20x.png) |
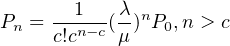 |
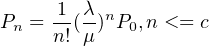 |
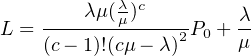 |
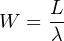 |
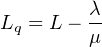 |
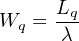 |
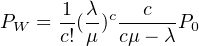 |
΄Ολοι μας έχουμε βιώσει την δυσάρεστη εμπειρία της αναμονής σε μία ουράμε σκοπό την εξυπηρέτησή μας για κάποια ανάγκη Δυστυχώς το φαινόμενο αυτό είναι ιδιαίτερα συνηθισμένο στις τεχνολογικά ανεπτυγμένες κοινωνίες. Περιμένουμε σε ουρές στην κίνηση στον δρόμο, στα διόδια, στα τηλεφωνικά κέντρα εξυπηρέτησης, στα ταμεία των supermarkets, στις τράπεζες, στα ταχυδρομεία κτλ. Στην αναμονή αυτή πελάτες ονομάζονται είτε τα φυσικά πρόσωπα, σε περιπτώσεις όπως οι ουρές των ταχυδρομείων και των τραπεζών, είτε τα αεροπλάνα, στην περίπτωση του αεροδρομίου, είτε δεδομένα σε ένα υπολογιστικό σύστημα κτλ. Στους πελάτες όπως είναι φυσικό δεν αρέσει αυτή η κατάσταση της αναμονής. Η ίδια κατάσταση είναι όμως δυσάρεστη και στους διαχειριστές συστημάτων όπως τα ανωτέρω,λόγω του γεγονότος ότι η αναμονή σε κάποια ουρά αυξάνει το λειτουργικό κόστος του συστήματος. ΄Αρα προκύπτει εύλογα το ερώτημα: “Γιατί λοιπόν να υπάρχει αναμονή;” Η απάντηση είναι απλή: ϒπάρχει μεγαλύτερη ζήτηση για εξυπηρέτηση από την εξυπηρέτηση που μπορεί να προσφέρει η υπάρχουσα υποδομή. Σε γενική περίπτωση,ένα σύστημα διαθέτει υπαλλήλους για την εξυπηρέτηση και έναν χώρο αναμονής με άπειρη ή περιορισμένη χωρητικότητα. Στην ουρά αναμονής υπάρχει τυχαιότητα τόσο στους χρόνους των αφίξεων των διαδοχικών πελατών όσο και στους χρόνουςεξυπηρέτησης κάθε πελάτη.Λόγω αυτής της τυχαιότητας,ο αριθμός των παρόντων πελατών στο σύστημα (μήκος ουράς) αυξομειώνεται ως συνάρτηση του χρόνου κατά τυχαίο τρόπο, είναι δηλαδή μια στοχαστική διαδικασία ή ανέλιξη. ΄Ετσι οι ουρές αναμονής αποτελούν ενα πεδιό εφαρμογής των στοχαστικών διαδικασιών και κατα επέκταση των μαθηματικών. [4] [3]
Η μελέτη των συστημάτων αναμονής ξεκίνησε από την
τηλεφωνία. Πρωτοπόρος ερευνητής ήταν ο Δανός
μαθηματικός A.K. Erlangο οποίος εργαζόταν στα Bell
Labs,ανέπτυξε τις βασικές αρχές της θεωρίας Ουράς και
το 1909 δημοσίευσε το “The Theory of Probabilities and
Telephone Conversations”. Το1927 ο E.C. Molina
δημοσίευσετο “Application of the Theory of Probability
to Telephone trunking problems” και ένα χρόνο αργότερα
ο Thornton Fry δημοσίευσε το “Probability and its
engineering users” το οποίο επεκτάθηκε πάνω στην
προηγούμενη δουλειά του Erlang.Στις αρχές του 1930 ο
Felix Pollaczek έκανε πρωτοπόρα δουλειά στην είσοδο
Poisson, στην αυθαίρετη έξοδο, και στα προβλήματα
μονών/ πολλαπλών καναλιών. Την ίδια περίοδο αντίστοιχη
δουλεία γινόταν στην Ρωσία από τους Kolmogorov και
Khintchine, στην Γαλλία από τον Crommelin και στην
Σουηδία από τον Palm. Μέχρι το 1950 η θεωρία ουρών
παρουσίαζε αργή ανάπτυξη αλλά στην συνέχεια γνώρισε
μεγάλη άνοδο. Στην δεκαετία του 1960 η θεωρία ουρών
ενισχύθηκε σημαντικά από τα επιστημονικά πεδία του
Computer engineering και των δικτύων επικοινωνίας
μέσω υπολογιστών. Στην επόμενες δεκαετίες η θεωρία
ουρών κατάφερε να συμβαδίσει με την μεγάλη ανάπτυξη
των υπολογιστικών συστημάτων, των δικτύων των
υπολογιστών και των δορυφορικών επικοινωνιών.Στην
σημερινή εποχή,δίνεται στην βιβλιογραφία μεγάλη έμφαση
στις ακριβείς λύσεις στα προβλήματα ουρών με την
χρήση έξυπνων μαθηματικών κόλπων. Με την βοήθεια
της μεγάλης υπολογιστικής ισχύος η οποία, λόγω
της ανάπτυξης των προσωπικών υπολογιστών είναι
διαθέσιμη στον καθένα τώρα πια, η θεωρία ουρών
αναπτύσσεται ραγδαία σε πολλούς τομείς της καθημερινής
ζωής. Η θεωρία ουρών χρησιμοποιεί την δημιουργία
μοντέλων και την άμεση χρήση των τεχνικών αυτών στη
διαχείριση της λήψης αποφάσεων. Είναι τόσο ισχυρή,
επειδή η πανταχού παρούσα κατάσταση των ουρών
σημαίνει ότι υπάρχουν αμέτρητες και διαφορετικές
εφαρμογές της. Μερικές απο αυτές συναντάμε σε τομείς
όπως:
[2] [8]
΄Ενα σύστημα αναμονής δέχεται πελάτες από μια πηγή
εισόδου.Ο αριθμός των πελατών, που εισέρχονται στο
σύστημα, μπορεί να είναι πεπερασμένος ή άπειρος.Το
σύστημα αναμονής περιλαμβάνει μια γραμμή αναμονής
(ουρά), η οποία αποτελείται από πελάτες, που περιμένουν,
αν όλες οι θέσεις εξυπηρέτησης είναι απασχολημένες. Αν
υπάρχουν περισσότερες παράλληλες και ανεξάρτητες
γραμμές αναμονής, τότε αυτές εξετάζονται ως διαφορετικά
και ανεξάρτητα συστήματα.Χαρακτηριστικά στοιχεία της
γραμμής αναμονής είναι το μέγιστο επιτρεπόμενο μήκος
και η πειθαρχία της.Αν και στις περισσότερες των
περιπτώσεων θεωρείται, ότι η ουρά μπορεί να έχει άπειρο
μήκος, υπάρχουν συστήματα, στα οποία ο χώρος, που
διατίθεται για την ουρά, είναι προκαθορισμένος και χωρά
ορισμένο αριθμό πελατών. Η πειθαρχία της ουράς
καθορίζει τη σειρά προτεραιότητας για την εξυπηρέτηση
του επόμενου πελάτη. Η πιο συνηθισμένη ονομάζεται
FCFS(FirstComeFirstServed). Παρόλα αυτά υπάρχουν και
άλλες πειθαρχίες όπως η LCFS(LastComeFirstServed)
και η τυχαία επιλογή του πελάτη προς εξυπηρέτηση
(SIRO, ServiceInRandomOrder). Τέλος, ο μηχανισμός
εξυπηρέτησης χαρακτηρίζεται κυρίως από τον αριθμό των
παράλληλων θέσεων εξυπηρέτησης στο σύστημα και την
κατανομή του χρόνου εξυπηρέτησης των πελατών, από
την έναρξη μέχρι την ολοκλήρωσή της. Μετά την
ολοκλήρωση της εξυπηρέτησης οι πελάτες αποχωρούν από
το σύστημα.Σύμφωνα με τα παραπάνω γίνεται κατανοητό,
ότι οι δυνατοί συνδυασμοί των χαρακτηριστικών στοιχείων
των συστημάτων αναμονής είναι πάρα πολλοί. Επομένως
χρησιμοποιείται μια συντομογραφία, που αποτελείται από
έξι σύμβολα Α/Β/c/k/m/z, για την περιγραφή του
κάθε συστήματος. Στη συντομογραφία αυτή, το c
χαρακτηρίζει τον αριθμό των εξυπηρετητών, ενώ τα Α και
Β καθορίζουν την κατανομή των χρόνων άφιξης κα
εξυπηρέτησης αντίστοιχα. Το σύμβολο k αντιπροσωπεύει
το μέγιστο αριθμό πελατών, που μπορούν να βρίσκονται
στο σύστημα.Τέλος,το σύμβολο m χαρακτηρίζει το
μέγεθος του πληθυσμού, από τον οποίο προέρχονται οι
αφίξεις και το z την πειθαρχία της ουράς. Για λογούς
απλούστευσης,θα παροουσιάσουμε το μοντέλο Μ/Μ/c (c
μονάδες εξυπηρέτησης).
Στο μοντέλο αυτό ισχύουν οι εξής προϋποθέσεις:
![P = ------------1------------
0 ∑cn-=10[ 1n!(λμ)n]+ 1c!(λμ)c(ccμμ-λ)](hw20x.png) |
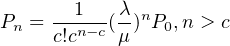 |
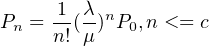 |
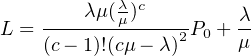 |
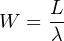 |
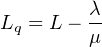 |
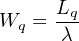 |
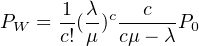 |
[7] [9] [1]
Σε ένα κομβικό σημείο ενός δικτύου με μία είσοδο
και τρεις εξόδους φτάνουν κατάμέσο όρο 20 πακέτα
δεδομένων το δευτερόλεπτο. Κάθε γραμμή εξόδου μπορεί
ναδεχτεί 10 πακέτα/sec. Ωστόσο, συχνά δημιουργείται
ουρά (τα πακέτααποθηκεύονται προσωρινά σε έναν
buffer) λόγω του ακανόνιστου ρυθμού αφίξεωντων
πακέτων.
α)Βρείτε το μέσο χρόνο αναμονής του πακέτου στο
buffer.
β)Ποια είναι η πιθανότητα να υπάρχουν το πολύ 2 πακέτα
συνολικά στο κομβικό σημείο (και σε αναμονή και στις
εξόδους);
ΛϒΣΗ
΄Εχουμε μοντέλο Μ/Μ/cμε c=3, λ=20 πακέτα/sec, μ =
10 πακέτα/sec.
α ) Ουσιαστικά ζητάμε το Wq. Προηγουμένωςμε βάση το
τυπολόγιο πρέπει να υπολογίσουμε τα Ρ0, L, Lq. ΄Εχουμε
c= 3 και λ/μ = 2, οπότε:
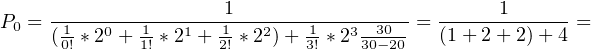 |
 |
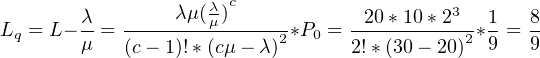 |
΄Αρα,
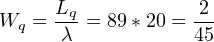 |
Συνεπώς,ο μέσος χρόνος αναμονής ενός πακέτου στον
buffer είναι 2/45sec.
β)Το πολύ 2 σημαίνει 0,1 ή 2. ΄Εχουμε Ρ0= 1/9 και από
τον τύπο
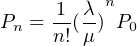 |
΄Εχουμε οτι:
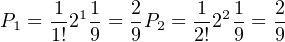 |
΄Αρα η πιθανότητα να υπάρχουν το πολύ 2 πακέτα στον κόμβο είναι:
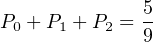 |
δηλαδή 55,55/100 [6] [5]
[2] Queuing theory: Definition, history real-life applications.
[3] STOQASTIKES ANELIXEIS. ΕΚΔΟΣΕΙΣ ΖΗΤΗ ΘΕΣΣΑΛΟΝΙΚΗ, 2003.
[4] A.Manou. ΣϒΣΤΗΜΑΤΑ ΕΞϒΠΗΡΕΤΗΣΗΣ ΜΕ ΜΕΤΑΒΑΛΛΟΜΕΝΕΣ ΠΑΡΑΜΕΤΡΟϒΣ-ϒΠΟΛΟΓΙΣΤΙΚΕΣ ΤΕΧΝΙΚΕΣ ΚΑΙ ΠΡΟΒΛΗΜΤΑ ΕΛΕΓΧΟϒ, 2014.
[5] D.Fakinoy. OURES ANAMONHS. ΕΚΔΟΣΕΙΣ ΣϒΜΜΕΤΡΙΑ, 2008.
[6] G.Kostaras. Θεωρία Ουρών, Μελέτη και Σύγκριση μοντέλων μιας ϒπηρεσίας, February,2012.
[7] G.Tzavelas. ΘΕΩΡΙΑ ΟϒΡΩΝ ΑΝΑΜΟΝΗΣ, 2019.
[8] X.ASVESTOPOYLOY. ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑΑΝΑΠΤϒΞΗ ΔϒΝΑΜΙΚΩΝ ΠΡΟΤϒΠΩΝ ΓΙΑ ΣϒΣΤΗΜΑΤΑ ΑΝΑΜΟΝΗΣ, 2016.